Final Exam
Date & Time
Wednesday, Decmeber 13, 8:00-9:50am, PM 110
Overview
The final exam is comprehensive will cover all material from the beginning of the semester through the end but with some emphasis on material covered since Test 2. The final is more comprehensive than Test 2 was. This material includes everything discussed in lectures and covered in assignments. You should know concepts (e.g. what an AVL tree is, how Dijksra’s algorithm works) as well as syntax. You may be asked to write, analyze, and/or debug code.
Format
- Multiple Choice
- Free Response
Topics
- Test 1 Topics
- Test 2 Topics
- Sorting Algorithms
- Binary Search
- Hashing
- Hash Table
- Hash Function
- Searching, Inserting, and Deleting
- Separate Chaining (Open Hashing)
- Probing (Closed Hashing)
- Graphs
- Terminology
- Undirected & Directed
- Depth-First Search
- Breadth-First Search
- Topological Sort
- Shortest Path Algorithms
- Minimum Spanning Tree Algorithms
Example Types of Free-Response Questions
- Test 1 Example Questions
- Test 2 Example Questions
- Which of the six search algorithms we discussed have O(n^2) complexity?
- Why is quicksort preferred over mergesort?
- Which type of probing (double, linear, quadratic) allows a higher load factor before the hash table needs to be rebuilt?
- Which class of integers are good lengths for hash tables? Why?
- Given the hash table below using probing, a hash function
h(x) = x % 7, and a quadratic conflict resolution strategy, which index does the valuex=27end up in?
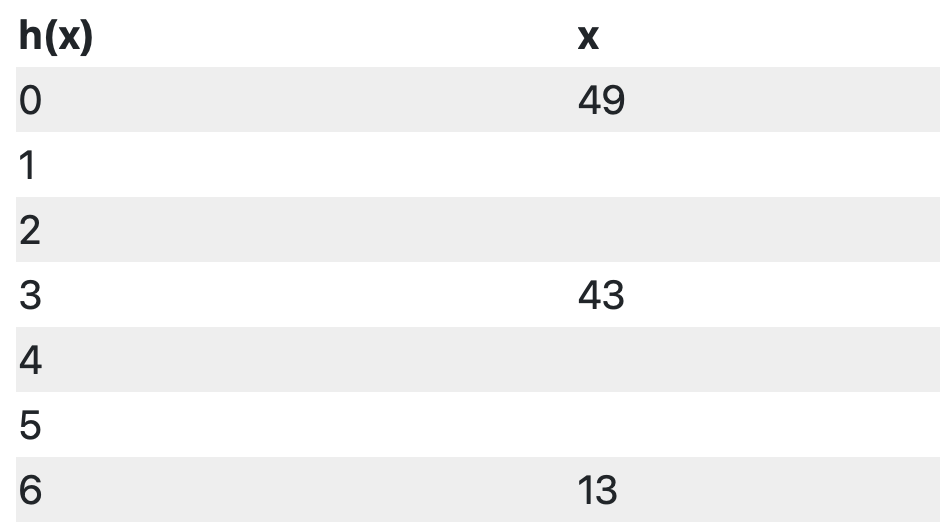
- When are adjacency matrices preferred over adjacency lists?
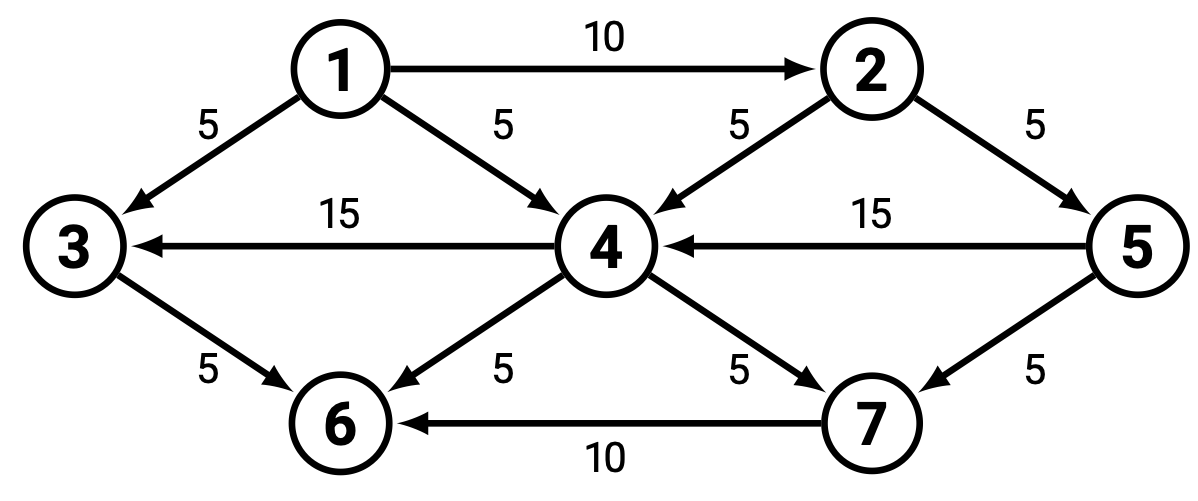
- How many edges are in the above graph?
- Is there a path from 3 to 2 in the above graph?
- What is the indegree of node 5 in the above graph?
- Identify a cycle in the above graph.
- Is the above graph strongly connected?
- Write the adjacency matrix for the above graph.
- What is the weighted shortest path from 2 to 6?
- What is a topological sort of the above graph?

- Write the depth-first search order of the above graph starting with A when the adjacency list is in alphabetical order.
- Write the breadth-first search order of the above graph starting with A when the adjacency list is in alphabetical order.
- Identify a spanning tree in the above graph.
- Does a path in the minimum spanning tree give the shortest distance between between any two nodes?