Assignment 2
In this assignment, you will write two short programs to solve problems using recursion.
1. Initial Setup
Log in to Unix.
Run the setup script for Assignment 2 by typing:
setup 2
The setup script will create the directory Assign2 under your csci241 directory. It will copy a makefile named makefile to the assignment directory and will also create symbolic links to a pair of test programs that you can use to verify that your output is correct.
Using the makefile we give you, you can build one specific program or build both programs. To build a single specific program, run the command make followed by the target name for the program that you want to build (hanoi or queens). For example:
z123456@turing:~$ make hanoi
To build both programs, run the command make all or just make.
Running the command make clean will remove all of the object and executable files created by the make command.
2. Towers of Hanoi
Legend has it that in a temple in the Far East, priests are attempting to move a stack of disks from one peg to another. The initial stack had 64 disks threaded onto one peg and arranged from bottom to top by decreasing size. The priests are attempting to move the stack from this peg to a second peg under the constraints that exactly one disk is moved at a time, and at no time may a larger disk be placed above a smaller disk. A third peg is available for temporarily holding the disks. According to the legend, the world will end when the priests complete their task.
Consider three pegs numbered 1 through 3. Let us assume that the priests are attempting to move the 64 disks from peg 1 to peg 2, using peg 3 as a temporary holding peg. The problem is to design an algorithm that that will print the precise sequence of disk peg-to-peg transfers.
If you were to approach this problem with conventional methods, you would rapidly find yourself hopelessly knotted up in managing the disks. Instead, if you attack the problem with recursion in mind, it immediately becomes tractable. If we assume that we have a function that can move n - 1 disks from one peg to another using a third peg as a temporary holding peg, then we can easily formulate an algorithm to move n disks from peg 1 to peg 2 by using the function that moves n - 1 disks as follows:
Move n - 1 disks from peg 1 to peg 3, using peg 2 as a temporary holding peg.
Move the last disk (the largest) from peg 1 to peg 2.
Move the n - 1 disks from peg 3 to peg 2, using peg 1 as a temporary holding peg.
Write a recursive program that solves the Towers of Hanoi problem. Your solution must be recursive to be eligible for any credit.
2.1. Input
Your program must accept a single command line argument, a positive integer. This integer n will represents the number of disks to move. Number the disks from 1 (the smallest disk) to n (the largest disk). You should always start with all the disks on peg 1 with pegs 2 and 3 empty. Your program should then produce the sequence of disk peg-to-peg moves to move all the disks from peg 1 to peg 2.
2.2. Output
Your output should print one move per line. Each move must be in the following format,
1 2->3
which is interpreted as "move disk 1 from peg 2 to peg 3." Assuming that the name of your program is hanoi, below is an example of what an execution of your program should look like:
z123456@turing:~$ ./hanoi 2
1 1->3
2 1->2
1 3->2
z123456@turing:~$
The format of the output must be exactly has shown above. There is another program (described below) that we have written to check the output of your program. It expects exactly this format.
WARNING: The number of moves it takes to transfer the disks from peg 1 to 2 grows exponentially as you increase the number of disks, (for n disks the number of moves is 2n - 1). If each move produces 7 bytes of output, redirecting the 20 disk output to a file will produce a 7MB file. Take care not to do that. It is safe to run your program with as many disks as you want as long as the output goes to the screen. But be careful not to redirect the stdout of your program for large disk counts, e.g., do not do the following,
z123456@turing:~/csci241/Assign2$ ./hanoi 20 > 20.out
If this does happen, don't panic. Simply remove the file using the command
rm 20.out
2.3. Files You Must Write
Write the code for this part of the assignment in a single file which must be called hanoi.cpp.
2.4. Files We Give You
If you use the setup command to get ready for this assignment, you will find an executable file called test_hanoi in your ~/csci241/Assign2 directory.
You can use test_hanoi to test the output of your program (rather then checking it by hand). test_hanoi reads the output (in the format described above) of hanoi and prints either "SUCCESS" or "failure". test_hanoi also takes a command line argument that must match the command line argument passed to hanoi that generated the output file.
You can run test_hanoi in one of two ways.
z123456@turing:~/csci241/Assign2$ ./hanoi 5 > 5.out
z123456@turing:~/csci241/Assign2$ ./test_hanoi 5 < 5.out
SUCCESS
z123456@turing:~/csci241/Assign2$
In this method you are storing the output from hanoi in a file called 5.out and then passing that file to test_hanoi. This should only be used for smaller runs, say problems with 10 or fewer disks. You might want to run hanoi this way while debugging; in case test_hanoi reports "failure", you can hand-inspect 5.out to find the error.
z123456@turing:~/csci241/Assign2$ ./hanoi 5 | ./test_hanoi 5
SUCCESS
z123456@turing:~/csci241/Assign2$
In this method you do not create an output file. The output of hanoi is "piped" directly as input to test_hanoi. Running large problems (many disks) with this method does not create large files but may take very long to execute. You're probably safe with disk counts < 20.
2.5. Hints
Consider writing a recursive function
void move(int n_disks, int src_peg, int dest_peg, int temp_peg)
3. Eight Queens
Write a program that places eight queens on a chessboard (8 x 8 board) such that no queen is "attacking" another. Queens in chess can move vertically, horizontally, or diagonally.
How you solve this problem is entirely up to you. You may choose to write a recursive program or an iterative (i.e., non-recursive) program. You will not be penalized/rewarded for choosing one method or another. Do what is easiest for you.
3.1. Output
Below is one solution to the eight queens problem, there may be others. Your program only needs to find one solution, any solution, and print it. Assuming the name of your program is queens, executing your program should look like this:
z123456@turing:~/csci241/Assign2$ ./queens
1 0 0 0 0 0 0 0
0 0 0 0 1 0 0 0
0 0 0 0 0 0 0 1
0 0 0 0 0 1 0 0
0 0 1 0 0 0 0 0
0 0 0 0 0 0 1 0
0 1 0 0 0 0 0 0
0 0 0 1 0 0 0 0
z123456@turing:~/csci241/Assign2$
where a '1'; means a queen is on that square of the board and a '0' means the square is empty.
Note that it is very important that your output be formatted exactly as shown above. In grading your program, its output will be checked by another program (we wrote) that expects as input a solution in this format.
3.2. Files You Must Write
Write the code for this part of the assignment in a single file which must be called queens.cpp.
3.3. Files We Give You
If you use the setup command to get ready for this assignment, you will find an executable file called test_queens in your ~/csci241/Assign2 directory.
You can use test_queens to test the output of your program (rather then checking it by hand). test_queens reads the output (in the format described above) of queens and prints either "SUCCESS" or "failure".
You can run test_queens in one of two ways.
z123456@turing:~/csci241/Assign2$ ./queens > queens.out
z123456@turing:~/csci241/Assign2$ ./test_queens < queens.out
SUCCESS
z123456@turing:~/csci241/Assign2$
In this method you are storing the output from queens in a file called queens.out and then passing that file to test_queens. You might want to run queens this way while debugging; in case test_queens reports "failure", you can hand-inspect queens.out to find the error.
z123456@turing:~/csci241/Assign2$ ./queens | ./test_queens
SUCCESS
z123456@turing:~/csci241/Assign2$
In this method you do not create an output file. The output of queens is "piped" directly as input to test_queens.
3.4. Hints
You might want to represent the chessboard using a 2-D array of integers or Boolean variables, e.g., int board[8][8] or bool board[8][8]. This array can be declared in your main() function or as a data member of a class that you write. Initialize the board by filling the array with 0s or false.
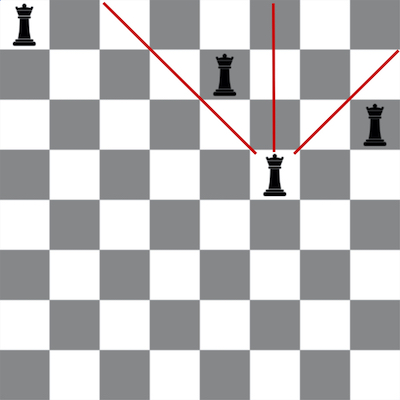A general strategy is to solve the problem by starting with the top row of the chessboard and proceeding down the chessboard one row at a time. Only place a single queen in each row. This eliminates the need to check for other queens on the same row (i.e., queens that could attack horizontally). Always start processing a row by attempting to place a queen in the leftmost column and then moving to the right as needed. When placing a queen in a particular row, remember that it suffices
to only check squares in the rows above you. For example, the red lines in the chess board image to the right illustrate the squares that must be checked for an existing queen when trying to place a new queen in the sixth column of the fourth row.
If the queen is safe in a particular column, then place it on the board at that column (board[row][col] = 1; or board[row][col] = true;) and proceed to the next row. If it is not safe, then continue to move one column to the right until you find a safe spot or you run out of columns.
There are two general ways that you can solve the eight queens problem: recursively or iteratively. Below are some more general hints that use the suggestions above, first in a recursive algorithm and then in an iterative algorithm. Although two general algorithms are discussed below, remember that you are only required to write one solution to this problem. Write as many solutions as you would like, but submit only one program for grading. You may elect to use the hints from either section below, or you may decide to ignore all of them and design a solution on your own. Whatever you decide is acceptable.
3.3.1. Recursive Algorithm
You could write a recursive function called place_queens() that returns a Boolean value and accepts two arguments, the chessboard and a row index. If your chessboard is a data member of a class, then this will be a member function of that class and you will only need to pass it the row index.
The way to think about place_queens() is that it attempts to place a queen in the row that you specified and all rows below that. If it can place all of the queens from that row down, it returns true and leaves the queens on the chessboard. If it couldn't, then it returns false and removes all the queens from that row down. This way, after you initialize the chessboard, you may make a single call from your main() routine like this
place_queens(board, 0); // Call a function
or this
q.place_queens(0); // Call a member function
(assuming that q is an instance of the class that you defined).
In either case, you need to check the return value of the function for success or failure.
place_queens() always starts by attempting to place a queen in the leftmost column of the row that it received as an argument and checking that it is safe from all the queens in the rows above it. If it is not safe, then proceed by moving the queen one column to the right and checking that square. If you get to the right end of the board without finding a safe spot, then return false. If you find a safe spot, then place the queen on the board and call place_queens() again (recursively) asking it to place all the queens on the rows below yours (i.e., passing it the same board it received but incrementing the row index by 1).
Test the return value of that recursive call. Recall that place_queens() will attempt to place all the queens in the rows below and return either false or true based on its success. If the return value is true, then simply return true yourself and you are done. If it is false, then there was no way to place the other queens on the board. You must try and find another safe column (to the right) in the same row. Move the queen in this row to the right, one column at a time, until you find another square where the queen is safe from all of the queens above it. If you find another safe column, place the queen there and make another recursive call to place_queens(). If there are no more safe columns in this row, then remove the queen from this row and return false.
The stopping condition for this recursive algorithm is when you enter place_queens() and the row that you have been passed in is greater than 7 (assuming that the top row is row 0).
3.3.2. Iterative Algorithm
Start by placing a queen in the leftmost column of the top row. Since there are no rows above the top row, there are no "attacking" queens to check, so proceed to the second row. As you move from the first row to the second row, we call this "approaching a row from the top". This is differs from "approaching a row from the bottom" (described below).
When approaching a row from the top, there are no queens on that row. Start by attempting to place the queen in the leftmost column and checking all of the rows above. If the queen is safe in that column, place it on the board and proceed to the next row. If it is not safe, try the next column to the right and check there. If you get to the end of the row without finding a safe column for the queen, you must back up a row. This requires you to go back to the previous row and move that queen to the right. This is what is meant by "approaching the row from the bottom".
When approaching a row from the bottom, there is already a queen placed on that row and it is already safe from all of the queens above it. The problem is that no more queens could be placed on the board in the rows below it. So this queen must be moved from its safe spot to another safe spot in the same row. All of the columns to the left of this queen have already been checked. The only place for this queen to go is to the right. Start by trying one square to the right and checking the rows above. If that column is safe, place the queen there and proceed to the row below, approaching it from the top. If it is not safe, keep moving the queen to the right. If you run out of columns, then remove the queen from the board and back up to the row above, approaching it from the bottom.