
A graph consists of a set of vertices and a set of edges. Vertices are the nodes that make up the graph. Edges, or arcs, connect the vertices.
There are two types of graphs:
A directed graph, or digraph, is a graph in which the edges connect vertices in a specific direction.
A directed graph with six vertices {1, 2, 3, 4, 5, 6} and ten directed edges {1 to 2, 1 to 4, 1 to 5, 2 to 3, 2 to 4, 3 to itself, 4 to 2, 4 to 3, 6 to 2, 6 to 3} can be pictured as:

A tree is a special case of a digraph. It is characterized by the fact that:
A digraph differs from a tree in that:
Some definitions that are associated with graphs:
Two vertices are said to be adjacent if there is an edge connecting them.
A path in a graph is a sequence of vertices and edges.
The length of a path is the number of edges on a path, which is always equal to the number of vertices - 1.
A loop is a path made up of an edge that goes from a vertex back to itself.
A simple path is a path where all of the vertices are distinct, with the exception of the first and last.
A cycle is a path of at least length 1 where the first and last nodes are the same. The edges must be distinct for undirected graphs.
A digraph is acyclic if it has no cycles.
A digraph is said to be strongly connected is there is a path from every vertex to every other vertex.
A complete graph is a graph in which there is an edge between every pair of vertices.
There are several ways of representing a graph. One of the most common is to use an adjacency matrix. To construct the matrix:
A directed graph and adjacency matrix:


An undirected graph and adjacency matrix
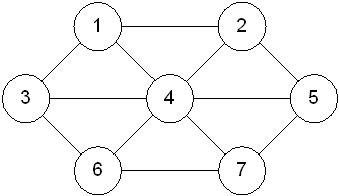
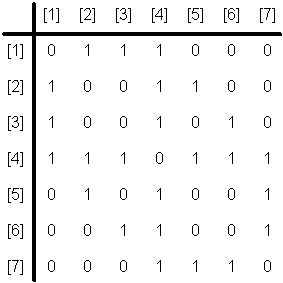
The space requirement for an adjacency matrix is V2, where V is the number of vertices.
One drawback to this type of representation is that it is often sparse, that is, it has a lot of zero entries, and thus considerable space is wasted.
To alleviate this problem, a graph can also be represented as an adjacency list. For this type of representation, an array is used to hold the data for each vertex in the graph. For each vertex, there is also a pointer to a linked list of all vertices that are adjacent to the vertex.
A directed graph and an adjacency list:

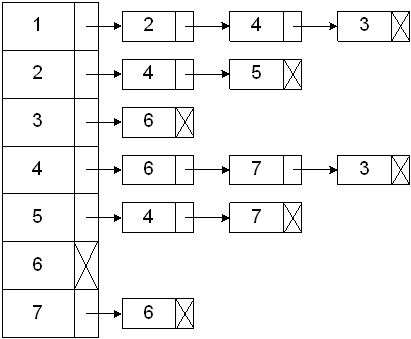
The space requirement for an adjacency list is E+V, where E is the number of edges and V is the number of vertices.
A topological sort is an ordering of vertices in a directed acyclic graph, such that if there is a path from vi to vj, the vi appears before vj in the ordering. This is not possible if the graph has a cycle.
Algorithm:
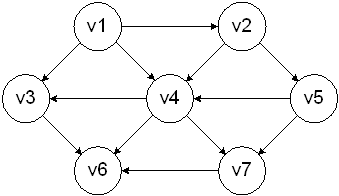
v1 v2 v5 v4 v3 v7 v6
v1 v2 v5 v4 v7 v3 v6
are both possible topological orderings.
The indegree of vertex v is the number of edges coming into v.
Assuming that the indegree for each vertex is stored and that the graph is stored as an adjacency list, the following algorithm can be derived:
for( counter from 0 through the number of vertices )
v = find a new vertex with indegree of 0
if v is not a vertex
error
endif
assign a topological number to v -- use the counter
for each vertex w that is adjacent to v
decrement w's indegree by 1
endfor
endfor
The finding of the vertex with indegree of 0 is accomplished by scanning the vertices looking for a vertex with indegree of 0 and no topological number. If no such vertex exists, then the graph contains a cycle.
Finding the vertex with indegree of 0 has a running time of V. That call is made V times, therefore the algorithm has a running time of V2.
The algorithm can be improved by simply storing all of the vertices with indegree of 0 on a queue. The new algorithm resembles:
for each vertex v
if v has indegree of 0
push v onto a queue
endif
endfor
Initialize a counter to 0
while the queue is not empty
pop the queue and assign to v
increment the counter
assign the counter as the topological number for v
for each vertex w that is adjacent to v
decrement w's indegree by 1
if w's indegree is 0
push w onto the queue
endif
endfor
endwhile
The algorithm now has a running time E+V since the for loop is executed at most once per edge, the queue operations are executed at most once per vertex, and the initialization is at most the size of the graph.
There are many ways to find the shortest path from one vertex to another.
the first assumes that the graph is weighted, which means that each edge has a cost to traverse it. The cost of a path is the sum of the edge costs, this is known as the weighted path length.
Single-source shortest path problem:
Given a weighted graph and a vertex s, find the shortest path weighted path from s to every other vertex in the graph.
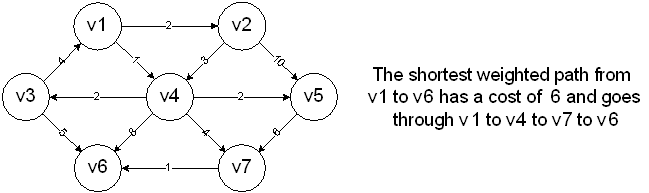
4 possible algorithms to find the shortest path from one vertex to all other vertices:
Choose a starting vertex and assign the value 0 to it.
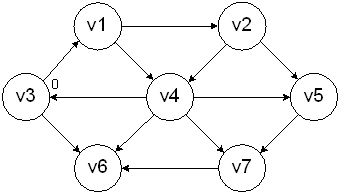
Look for all vertices that are a distance 1 away from the start and mark them as such.
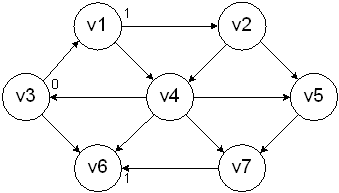
Repeat the process until all of the nodes are marked.
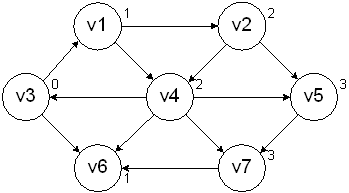
This type of processing is known as a breadth-first search, since it is processing vertices in layers. This is equivalent to a level-order traversal for trees.
To implement this, keep track of three pieces of information:
start vertex distance is 0
for dist of 0 through number of vertices
for each vertex v
if v has not been processed and v's distance is equal to dist
indicate that v has been processed
for each vertex w that is adjacent to v
if w's distance is not known
set w's distance to dist plus 1
set w's preceding vertex to v
endif
endfor
endif
endfor
endfor
The algorithm has a running time of V2 because of the nested for loops, but it can be improved by using a queue. The vertices will be pushed on the queue in the order of increasing distance from the start.
push the start vertex onto queue
set start vertex distance is 0
while the queue is not empty
v = pop the queue
indicate that v has been processed
for each vertex w that is adjacent to v
if w's distance is not known
set w's distance to dist plus 1
set w's preceding vertex to v
push w onto the queue
endif
endfor
endwhile
The algorithm now has a running time of E + V.
Using the graph from above results in the following:


After popping v3:


After popping v1:
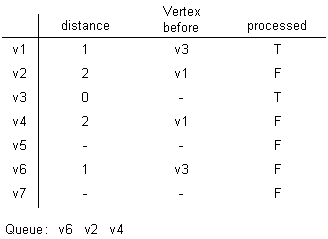
After popping v6:

After popping v2:

After popping v4:
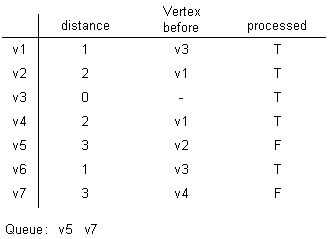
After popping v5:

After popping v7:
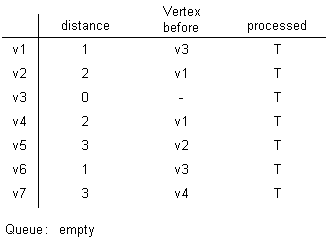
With this algorithm, the graph is weighted and it uses the same three principles as the previous algorithm:
It proceeds in stages. At each stage, a vertex is selected that has the smallest cost among all unprocessed vertices and mark the vertex as processed (ie. that the shortest path has been found).
The start vertex is v1. It is assigned a cost of 0 and marked to indicate it has been processed:
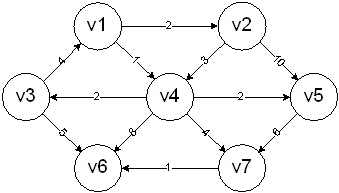
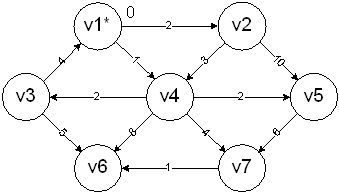
v2 and v4 are adjacent so they are adjusted accordingly:
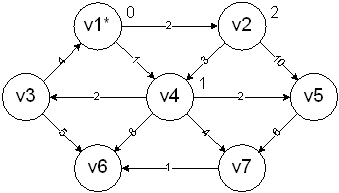
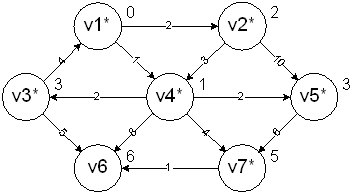
v4 is processed next since it has the smaller cost. It is marked as known and vertices v3, v5, v6, and v7 are adjusted accordingly:
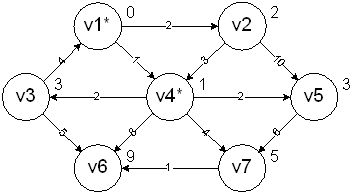
v2 is processed next. It is marked as known and vertices v4 and v5 are adjusted accordingly. v4 is left alone since it has already been processed. v5 is left alone because it already has a minimal cost:

v5 is processed next since it has the smallest cost. It is marked as known and vertex v7 is the adjacent vertex. It's left alone because the cost is already minimal:
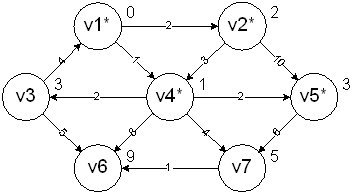
v3 is processed next since it has the smallest cost. It is marked as known and vertex v6 is the adjacent vertex. It's adjusted with the smaller cost:

v7 is next. v6 is again the adjacent and it's updated with the smaller cost:
v6 is next. There are no adjacent vertices so the processing is done:
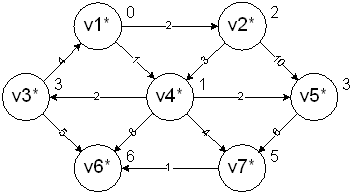
This algorithm is known as a greedy algorithm, because it solves the problem in stages by doing what appears to be best at each stage.
With this algorithm, the graph is still weighted but it is now possible to have an edge with a negative weight. The addition of the negative costs causes Dijkstra's algorithm to fail because once a vertex is processed, it is never processed again. But with a negative cost, it's possible that a path back to a vertex that costs less can be found.
To fix the problem: the weighted and unweighted algorithms will be combined. This drastically increases the running time!
To do this, the vertices will no longer be marked as processed.
Dijkstra's algorithm can be improved if the graph is known to be acyclic. The improvement is made by changing the order that the vertices are processed. It will now be done in a topological order.
This works because once a vertex is selected its cost cannot be lowered since it will no longer have any incoming edges from unprocessed vertices.